A 2021-es tavaszi vizsgaidőszak matematika érettségi feladatai

Két szinten lehet érettségi vizsgát tenni matematikából. Az egyszerűbb és természetesen a nehezebb közül lehet választani. A magasabb szintű vizsgához 10 kurzust kell kötelezően elvégezni, míg az egyszerűbbhöz hatot. Azaz ha valakinek hosszabb távú tervei vannak a tantárggyal, felvételihez, továbbtanuláshoz szeretné használni, természetesen a magasabb szintűt választja. 

Az összesen három: A, B1 és B2 nagyobb részből álló feladatlapban 13 feladat van, melyekből 10-et kell megoldani a következő módon. Az A részben levő összes, azaz négy feladat megoldása mindenkinek kötelező, a B1-ben 5-ből 3-at, a B2-ben pedig 4-ből 3-at kell megoldani. Minden feladat 0-12 pontig értékelnek, így az összpontszám 120. 

Mint az előzőekben is írtuk, a diákok elektronikus felületen vizsgáznak. Az “A” rész megoldásánál alapprogramokat és a vizsgához megadott táblázatot szabad használni, és csak ennek a leadása után lehet használni a “B” részhez tartozó, és ahhoz engedélyezett többféle programot, mint például Geogebra, Texas Instruments TI-Nspire CAS, wxMaxima, LoggerPro, LibreOffice Math, ChemSketch. A “B” részeket meg lehet oldani az “A” rész leadása nélkül is, de ekkor természetesen a “B” részhez engedélyezett programokhoz nincs a diáknak hozzáférése. 

Megoldóverseny középiskolásoknak!

Vegyél részt megoldóversenyünkön és nyerd meg a Finn minta ajándékcsomagok egyikét!

A 2021-es finn matek érettségi feladatsor 3 szabadon választott feladatát hibátlanul megoldók között sorsoljuk ki a 3 nyertest!

Oldj meg tetszés szerint 3 feladatot és küldd meg nekünk az eredményt a finnminta@gmail.com-ra! Az e-mail tárgyának a következőt add meg: ‘finn matek érettségi‘. A megoldásokat 2021. május 28-ig várjuk. Sorsolást 2021. május 29-én tartunk.

Nyereménycsomag tartalma: finn csokoládé, Finn minta maszk és matricák, @Lapland UAS PopSocket és ingyenes finn továbbtanulási tanácsadás.
A versenyen való részvétellel elfogadod a Finn minta adatkezelési tájékoztatóját.

Az “A” rész feladatai

Számold ki! Mindegyik kérdés 2 pontot ér

120 euróba kerül egy hangszóró. Mennyi az ára 30 % kedvezménnyel?

Az alább látható feladathoz két megoldást írtunk. Melyik a helyes?
Feladat: Hány százalékkal több a 210 a 200-nál?

1, megoldás: 210/200 = 1,05; 1,05 – 1 = 0,05. Válasz: 5%.

2, megoldás: 200/210 = 0,95; 1 – 0,95 = 0,05. Válasz: 5%.

Egy termék árához hozzáadjuk a 24 %-os áfát. Mennyi az áfa aránya a termék eladási árához viszonyítva százalékban kifejezve?

---

2. Focimatematika 

A labdarúgó pálya kapuja 7,32 m széles. A gólvonal közepétől 11,0 m-re, arra merőlegesen található a tizenegyes pontja. Mekkora nagyságú szögben látszik a büntetőrúgás pontjától a kapu? A szöget a pálya felszínén nézzük. (aineisto 2.A itt megadnak hozzá egy felülnézeti rajzot is) 

3. Képletek

A matematikai alkalmazásokban különféle képleteket használnak. A feladat:
Választhatsz! Fejezd ki az első 4 pontban megadott képletből az adott ismeretlent!
VAGY
Oldd meg az utolsó két pontban található feladatot!

4. Egyenesek 

A képen (4.A) hat egyenes és három pont látható. Alább a hat egyenes egyenlete olvasható. Állapítsd meg, hogy az adott egyenletnek megfelelő egyenes szerepel-e az ábrán, ha igen, az A vagy a B vagy a C ponton halad-e át.

A “B1” rész feladatai

5. Jegybevétel

A bajnokságra 4 802 jegyet adtak el. A főlelátóra 35 euró egy jegy, a felső- és az oldallelátóra 25 euró. Összesen 136 900 euró értékben adtak el jegyet. Hányan ültek a főlelátón? (12 pont)

6. Autók szén-dioxid kibocsátása

Az autók szén-dioxid kibocsátását gramm/km-ben adják meg. Az EU az új autók károsanyag kibocsátási határát 2030-ig a következőképpen határozta meg:

Év	Kibocsátás
2015	130 g/km
2020	95 g/km
2025	15 %-kal alacsonyabb, mint 2020-ban
2030	37,5 %-kal alacsonyabb, mint 2020-ban

1.Hány százalékkal kevesebb a kibocsátási határ 2020-ban 2015-höz viszonyítva? Egy tizedesjegy pontossággal válaszolj! (4p)

2.Hány százalékkal kisebb az elérni kívánt kibocsátás 2030-ban 2025-höz képest? Egy tizedesjegy pontossággal válaszolj! (4p)

3.Programalkalmazást használva készíts oszlopdiagrammot a 2015, 2020, 2025, 2030-as évek kibocsátásáról! (4p)

7. Kenó játék

A Kenó játékban 20 számot sorsolnak 70 számból. A 4-es típusban 4 számot választanak a 70-ből. Ily módon 916 895 különböző sort kapunk. A „3 találat” eredmény azt jelenti, hogy a kiválasztott számok közül 3 tartozik a kisorsolt 20-as csoportba, és így tovább. A nyereményt  úgy kapjuk meg, hogy a kiválasztott fogadást megszorozzuk az eredménytényezővel

(aineisto 7.A).

1. Mi a sor legvalószínűbb eredménye? És a legvalószínűtlenebb? (2p)

2. Matti egy sort játszik meg, tétje 3 euró. 4-et talál el. Mekkora összeget nyer? (2p)

3. Matti két sort játszik meg. Mi annak a valószínűsége, hogy az egyik sorban 4 találata lesz, a másikban pedig egyáltalán nem lesz találata? 

4. Hogyan számolják ki, hogy a 4 találatos sorokból 4 845 van? (4p) 

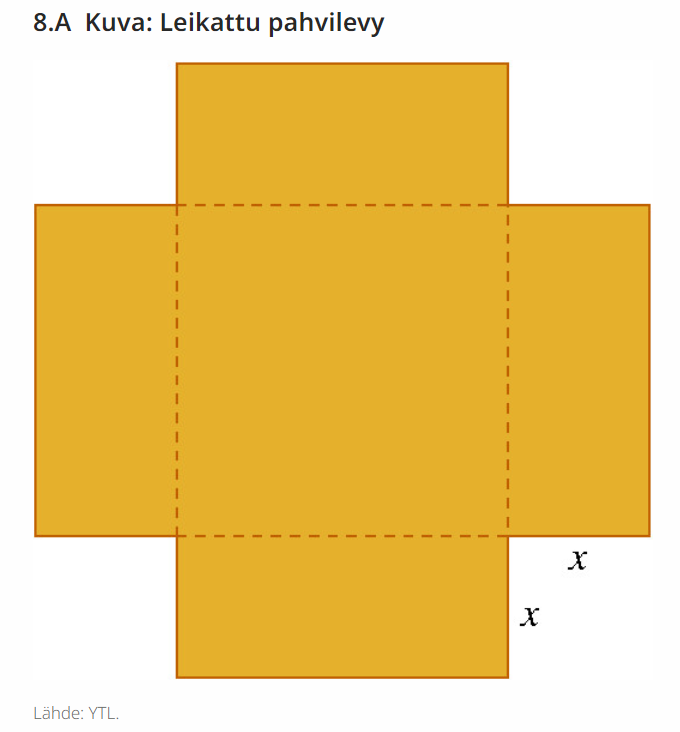
8.Készítsünk dobozt!

Egy négyzet alakú kartonlap oldalainak hossza 1,0 m. Mindegyik sarkából vágjunk le egy kisebb négyzetet, melynek oldalának hossza x. Ezután mind a négy  szélén maradt téglalap alakú részt hajtsunk fel 90 fokkal felfelé, és ragasszuk össze az egymás melletti oldalakkal úgy, hogy egy tető nélküli téglalap alakú dobozt kapjunk. Az x változó mekkora értékénél lesz ennek a doboznak a térfogata a lehető legnagyobb?

9.A pí

A táblázatban (9.A) a pí első 297 tizedes helye látható, melyekből három , 99 számjegyből álló csoportot alkottunk. Állapítsd meg az így kialakított 99 számjegynek a:

tartományát (2 p.)

móduszát, mediánját  (3 p.)

átlagát és szórását  (3 p.)

Gondold át, kiderül-e ebből a mellékletből, hogy ez a 99 szám átlagos/normális eloszlás szerint alakult-e ki?  (4 p.)

A “B2” rész feladatai

10.A kutya életkora

Egy régi felfogás szerint ha a kutya életkorát emberi évekre szeretnénk átszámolni, 7-tel kell szoroznunk. Például a legidősebb emberek 100 évesnél idősebbek, azonban a kutyák ritkán élnek húsz évnél tovább. Az utóbbi időben más módot is találtak a kutyák életkorának a meghatározására.

Vizsgáljuk meg a következő modellt, mely a logaritmuson alapul.

Ha a kutya tényleges kora t (év), akkor a 10-es alapú logaritmus segítségével 37 lg ⁡ t + 31 tudjuk kiszámolni az ennek megfelelő emberi életkort.

1. A kutya 2 éves. Mennyinek számít ez emberi életkorban a fenti példa alapján? (3 p.)

2. A kutya emberi években mért életkora 25 év a fenti modell alapján, hány éves valójában a kutya? (3 p.)

3. Becsüld meg, hogy mennyire megfelelően működik a modell alacsony és magas életkor esetén? (6 p)

11.Becslés

A könyvekben kínált bölcsességben megcsömörlött docens az összes könyvét el akarja adni az antikváriumnak, ezért meg kell becsülnie, hány darab könyve van. 

Három véletlenszerű méréssel a következő eredményeket kapja:
1, mérés: 25 könyv összesen 65,0 cm
2.mérés: 28 könyv összesen 76,0 cm
3.mérés: 14 könyv összesen 30,0 cm

E három mérésből melyikben vannak az átlagosan legvastagabb könyvek? (3 p.)

Összesen 38,07 méternyi könyv van a polcon. A docens az első pontban mért eredmények alapján becsli meg a könyvek összmennyiségét. Ehhez kétféle módszeren gondolkodik:

1.módszer: Elosztja a 38,07 hosszot az első pontban kiszámolt átlagok átlagával.

2.módszer: Kiszámolja a három mérés könyvmennyiségét és összvastagságát, így megkapja az átlagos könyvvastagságot, majd elosztja a 38,07 m hosszt a kapott számmal.

Számold ki mindkét eljárással a könyvek összmennyiségét, és becsüld meg, melyik módszer a hatékonyabb. (9 p.)

12.Lakásvásárlás

Jessi lakást vásárol. Két lakást is talált, amely elnyerte a tetszését. Azon gondolkodik, hogy anyagilag melyik lehetőség lenne számára a legkedvezőbb. A lakásokról a következőket tudjuk:

1.lakás:2 szoba + konyha, 47 m2, eladási ár: 89 000 €, közös költség 220 €/hó

2.lakás: 1 szoba + amerikai konyha + szauna, 42 m2, eladási ár: 96 000 €, közös költség 147 €/hó

1, Számold ki a lakások négyzetméter árát!(2 p.)

2, Jessinek 19 000 euró megtakarítása van. A lakás megvásárlásához szükséges további összegre 10 évre szóló kölcsönt venne fel, melynek 2, 4 % az éves kamata. Mennyit fizet Jessi a tíz év alatt a kamatra, és a közös költségre? Mindkét lakás esetében számold ki az összeget havi törlesztés esetén. A kölcsönt havonta törleszti.(7 p.)

3, Fogalmazd meg, és írd le, milyen egyéb tényezőket kell figyelembe venni, ha részletesebben akarod értékelni e két lakhatási lehetőség általános megfizethetőségét.  (3 p.)

13.Függvények

Tanulmányozzuk a függvények grafikonjait.